Energy Savings Formula

Mar 15 2021
In 2002, I became a firefighter in the north suburbs of Chicago. I was young and idealistic – loving almost every part of the job. However, I had another secret passion – sustainability.
In addition to running multiple gardens, compost bins, and even analysis on the best route and methodology to refuel our trucks – I was obsessed with our lighting.
I would walk into our apparatus bay, which had at the time High Output 8ft T12s. At first, I used to wonder why we left the lights on all night long. I learned why when I started turning them off – and they took forever to warm up for late night emergencies and crews would yell at me as they struggled to get to their truck or ambulance as the lights warmed up.
But then, I began to get really curious about what the lights actually consumed in terms of energy. I started writing out mathematical equations, and even bought a device to plug in and measure all kinds of gadgets at the firehouse that consumed electricity. I was far from an engineer, but had a ton of curiosity and instinct that there was waste occurring all around me.
In 2006, I began to study environmental policy at the University of Chicago Harris School of Public Policy. The best part of the program was the intense soccer that we played on the midway with students from all over the world, including Chile, Mexico, China, and Columbia. The second best part was the ability to take undergraduate science and economics courses with some of the best professors in the world.
My most impactful course was called Energy and Technology and taught by Elisabeth Moyer. It covered a ton of ground, was intense mathematically, and really taught the basics of energy.
I was struck by the most basic formulas, which I will cover here. KwH (kilowatt-hour) is a unit of energy and a commonly used term, but I didn’t really understand it. KwH is the power consumption over time, while kW (kilowatt) is an instantaneous measurement.
The most basic example that stuck with me was that a 100 watt incandescent light bulb uses 0.1 kW when it is on. If that bulb was on for an hour, it would be 0.1k Wh. If it was on for 100 hours, it would use 10 kWh.
Electricity is sold to consumers by the kWh, typically around ten cents per kWh. Usually higher in the NE and West Coast, with rates as high as $.40 per kWh in Hawaii. Rates in Texas during the recent power outage would be astronomical, if we paid rates that fluctuated. But $.10 per kWh is a good general place to start for understanding the math.
In the previous example, it would cost $1.00 to run a 100w bulb for 100 hours.
100 watts x 100 hours = 10,000 watts/hr
10,000/1,000 watt per kWh = 10 kWh
10 kW x $.10 = $1.00
Now, this only tells you what something currently uses (we call this current state). To find a justification for an investment into energy efficiency, you must measure the delta (or difference) of the new energy efficient product vs the older inefficient product.
In my fire station example, the 8ft T12 High Output lamp uses 110W. There are two per fixture, and the ballast that powers them also uses some energy. Our local utility, Comed, uses the default wattage of 232 watts in the Small Business Offering. That means that each lamp uses 110, and the ballast uses 12 watts (110 + 110 + 12 = 232). The actual usage is likely higher, as ballast can pull as much as 40 watts in a fixture like this. But this is a good rough estimate.
The apparatus bay had 24 fixtures, each fixture used 24 hr * 232 w = 5,528 watt hours per day, or 5.5 kWh. If the fire station was paying for them, which they were not because of a rate payer easement, they would cost $.55 per day per light. We had tons of those – likely close to 40. Over a year (365 days), each fixture would use:
24 hr * 232 w * 365 days / 1000 = 2032 kWh or $203 per year in cost.

There are a million ways to replace those fixtures with LEDs today. Years ago, there were T8 replacements. Those fixtures would typically use 4 32W (128 watts total) lamps to replace 2 110W HO lamps (232 watts). So the reduction in a T12 to T8 replacement would be 232 – 128 = 104 watts. Over 24 hours per day, 365 days per year, that savings would be:
104 watts saved * 24 * 365 / 1000 watts per kWh = 911 kWh annually, or roughly $90 per year per fixture.
Today’s LED equivalent ranges, but there are 13 W LED tubes that put out the same light as a 32 W T8. Four lamps – 52 watts, putting out the same light as a 232 W T12 HO.
232 – 52 = 180 * 24 * 365 / 1000 = 1576 kWh or $158 annually.
This same formula can be used across any energy efficiency upgrade, including anything that draws wattage. It can be more complex in HVAC or refrigeration, which can draw variable power at different times. However, even those have a simplicity in their math.
Featured Posts

May 02 2019
Verde Energy Efficiency Experts 10 Most Sustainable Companies in Chicago
In our energy efficiency consulting firm, we constantly look for inspiration from local companies that lead and innovate in clean energy and sustainability. Not all companies have billion dollar budgets, but that doesn’t mean that…
Continue Reading >
Related Articles

Jan 30 2026
Comprehensive Guide to 2026 Utility Energy Efficiency Rebates and Incentives
The beginning of 2026 has brought a new urgency to energy efficiency and building upgrades, and we want to share the key steps many of our customers are taking this year. As always, our business…
Continue Reading >
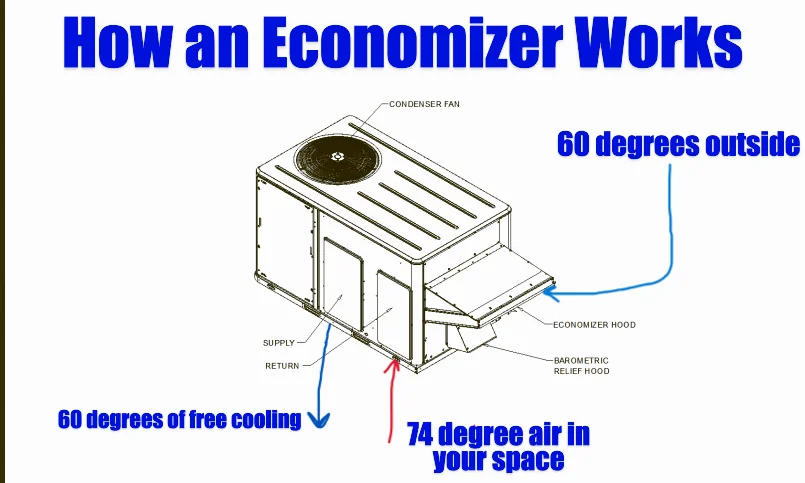
May 13 2025
Advanced Rooftop Controls for Your Building
Growing up, my grandmother was an influential person in my life. She believed in me when I started my business – when everyone else thought I was nuts to leave my steady job at the…